Elementarne iskaze možemo predstaviti čvorovima, a implikacije granama grafa. Svi čvorovi dostižni iz nekog čvora koji odgovara dokazanom tvrđenju odgovaraju tvrđenjima koja mogu biti dokazana primenom implikacija.
Jednostavan slučaj je kada u grafu nema ciklusa, tj. kada je u pitanju usmereni aciklički graf (engl. directed acyclic graph, DAG). Potrebno je i dovoljno dokazati samo ona tvrđenja koja se ne javljaju na desnoj strani nijedne implikacije, tj. samo ona tvrđenja kojima odgovaraju čvorovi grafa ulaznog stepena 0. Zaista, ta tvrđenja ne mogu biti dokazana primenom implikacija (jer nijedna implikacija ne vodi do njih), dok sva ostala tvrđenja mogu biti dokazana primenom implikacija (pošto nema ciklusa, prateći grane unazad, doći će se do nekog čvora čiji je ulazni stepen 0).
Slučaj grafa koji sadrži cikluse je donekle komplikovaniji. Primetimo da za svaku komponentu jake povezanosti grafa važi da je dovoljno dokazati bilo koji njen čvor i tada će sigurno biti moguće dokazati i sve ostale njene čvorove (jer su svi čvorovi u komponenti uzajamno dostižni). Zato je moguće izvršiti redukciju grafa, tj. napraviti kondenzovani graf u kom je svaka komponenta povezanosti predstavljena pojedinačnim čvorom. Kondenzovan graf je uvek aciklički i na njega možemo primeniti rešenje za aciklički graf. Na narednoj slici je prikazan graf iz primera ovog zadatka, kao i njegov kondenzovani graf, koji za čvorove ima tri komponente jake povezanosti polaznog grafa.
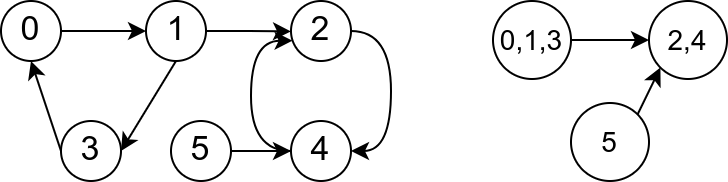
Ilustracije radi, u narednoj implementaciji eksplicitno gradimo kondenzovani graf (doduše, za rešenje ovog zadatka to nije neophodno, već je dovoljno samo prebrojati ulazne stepene njegovih čvorova).
// graf implikacija
vector<vector<int>> susedi;
// redni broj trenutne komponente jake povezanosti
int brojKomponenata = 0;
// preslikavanje čvorova u redne brojeve njihovih komponenata
vector<int> komponente;
// liste suseda u kondenzovanom grafu u kome su čvorovi komponente jake povezanosti
// polaznog grafa
vector<vector<int>> susedneKomponente;
// određuju se komponente jake povezanosti i gradi se kondenzovani graf
// liste povezanosti ovog grafa se smeštaju u globalnu promenljivu susedneKomponente
void napraviKondenzovaniGraf() {
// određuju se komponente jake povezanosti
// broj komponenata je sadržan globalnoj promenljivoj brojKomponenata
// komponenta svakog čvora je određena globalnim nizom komponente
odrediKomponente();
// broj čvorova kondenzovanog grafa je broj komponenata jake povezanosti
susedneKomponente.resize(brojKomponenata);
// grane koje su već dodate u kondenzovani graf
set<pair<int, int>> dodateGrane;
// prolazimo kroz sve grane originalnog grafa
for (int cvor = 0; cvor < susedi.size(); cvor++)
for (int sused : susedi[cvor]) {
// u kondenzovani graf dodajemo granu između komponente čvora i
// komponente suseda (ako nije već dodata)
if (komponente[cvor] != komponente[sused] &&
dodateGrane.count({komponente[cvor], komponente[sused]}) == 0) {
susedneKomponente[komponente[cvor]].push_back(komponente[sused]);
dodateGrane.emplace(komponente[cvor], komponente[sused]);
}
}
}
int main() {
// ucitavamo podatke o iskazima i implikacijama
// ...
// pravimo kondenzovani graf u kome su cvorovi komponente povezanosti
napraviKondenzovaniGraf();
// određujemo ulazne stepene čvorova kondenzovanog grafa
vector<int> ulazniStepen(susedneKomponente.size(), 0);
for (int cvor = 0; cvor < susedneKomponente.size(); cvor++)
for (int sused : susedneKomponente[cvor])
ulazniStepen[sused]++;
// brojimo čvorove čiji je ulazni stepen nula
int broj = 0;
for (int cvor = 0; cvor < susedneKomponente.size(); cvor++)
if (ulazniStepen[cvor] == 0)
broj++;
cout << broj << endl;
return 0;
}#include <iostream>
#include <vector>
#include <algorithm>
#include <stack>
#include <set>
using namespace std;
// graf implikacija
vector<vector<int>> susedi;
// redni broj trenutne komponente jake povezanosti
int brojKomponenata = 0;
// preslikavanje čvorova u redne brojeve njihovih komponenata
vector<int> komponente;
// pomocne strukture podataka za određivanje komponenata jake povezanosti
// da li je cvor posecen
vector<bool> posecen;
// dolazna numeracija čvorova
int vremeDolaska = 0;
vector<int> dolazniBroj;
// najniži dostižni čvor povratnom ili poprečnom granom unutar komponente
vector<int> lowlink;
// pomoćni stek i podatak o tome da li je čvor na steku
stack<int> tarjanStek;
vector<bool> naSteku;
// rekurzivna funkcija koja implementira Tarjanov algoritam
void tarjan(int cvor) {
posecen[cvor] = true;
dolazniBroj[cvor] = vremeDolaska++;
lowlink[cvor] = dolazniBroj[cvor];
tarjanStek.push(cvor);
naSteku[cvor] = true;
for (int sused : susedi[cvor]) {
if (!posecen[sused]) {
tarjan(sused);
lowlink[cvor] = min(lowlink[cvor], lowlink[sused]);
} else {
if (naSteku[sused])
lowlink[cvor] = min(lowlink[cvor], dolazniBroj[sused]);
}
}
if (dolazniBroj[cvor] == lowlink[cvor]) {
int cvorNaSteku;
do {
cvorNaSteku = tarjanStek.top();
tarjanStek.pop();
naSteku[cvorNaSteku] = false;
komponente[cvorNaSteku] = brojKomponenata;
} while (cvorNaSteku != cvor);
brojKomponenata++;
}
}
// određuje komponente povezanosti i smešta rezultat u globalni niz komponente
void odrediKomponente() {
// alociramo potrebnu memoriju i inicijalizujemo strukture podataka
int n = susedi.size();
posecen.resize(n, false);
komponente.resize(n);
dolazniBroj.resize(n);
lowlink.resize(n);
naSteku.resize(n, false);
// pokrećemo Tarjanov algoritam iz svakog neposećenog čvora
for (int cvor = 0; cvor < n; cvor++)
if (!posecen[cvor])
tarjan(cvor);
}
// liste suseda u kondenzovanom grafu u kome su čvorovi komponente jake povezanosti
// polaznog grafa
vector<vector<int>> susedneKomponente;
// određuju se komponente jake povezanosti i gradi se kondenzovani graf
// liste povezanosti ovog grafa se smeštaju u globalnu promenljivu susedneKomponente
void napraviKondenzovaniGraf() {
// određuju se komponente jake povezanosti
// broj komponenata je sadržan globalnoj promenljivoj brojKomponenata
// komponenta svakog čvora je određena globalnim nizom komponente
odrediKomponente();
// broj čvorova kondenzovanog grafa je broj komponenata jake povezanosti
susedneKomponente.resize(brojKomponenata);
// grane koje su već dodate u kondenzovani graf
set<pair<int, int>> dodateGrane;
// prolazimo kroz sve grane originalnog grafa
for (int cvor = 0; cvor < susedi.size(); cvor++)
for (int sused : susedi[cvor]) {
// u kondenzovani graf dodajemo granu između komponente čvora i
// komponente suseda (ako nije već dodata)
if (komponente[cvor] != komponente[sused] &&
dodateGrane.count({komponente[cvor], komponente[sused]}) == 0) {
susedneKomponente[komponente[cvor]].push_back(komponente[sused]);
dodateGrane.emplace(komponente[cvor], komponente[sused]);
}
}
}
int main() {
// ucitavamo podatke o iskazima i implikacijama
int n;
cin >> n;
susedi.resize(n);
int m;
cin >> m;
for (int i = 0; i < m; i++) {
int a, b;
cin >> a >> b;
susedi[a].push_back(b);
}
// pravimo kondenzovani graf u kome su cvorovi komponente povezanosti
napraviKondenzovaniGraf();
// određujemo ulazne stepene čvorova kondenzovanog grafa
vector<int> ulazniStepen(susedneKomponente.size(), 0);
for (int cvor = 0; cvor < susedneKomponente.size(); cvor++)
for (int sused : susedneKomponente[cvor])
ulazniStepen[sused]++;
// brojimo čvorove čiji je ulazni stepen nula
int broj = 0;
for (int cvor = 0; cvor < susedneKomponente.size(); cvor++)
if (ulazniStepen[cvor] == 0)
broj++;
cout << broj << endl;
return 0;
}